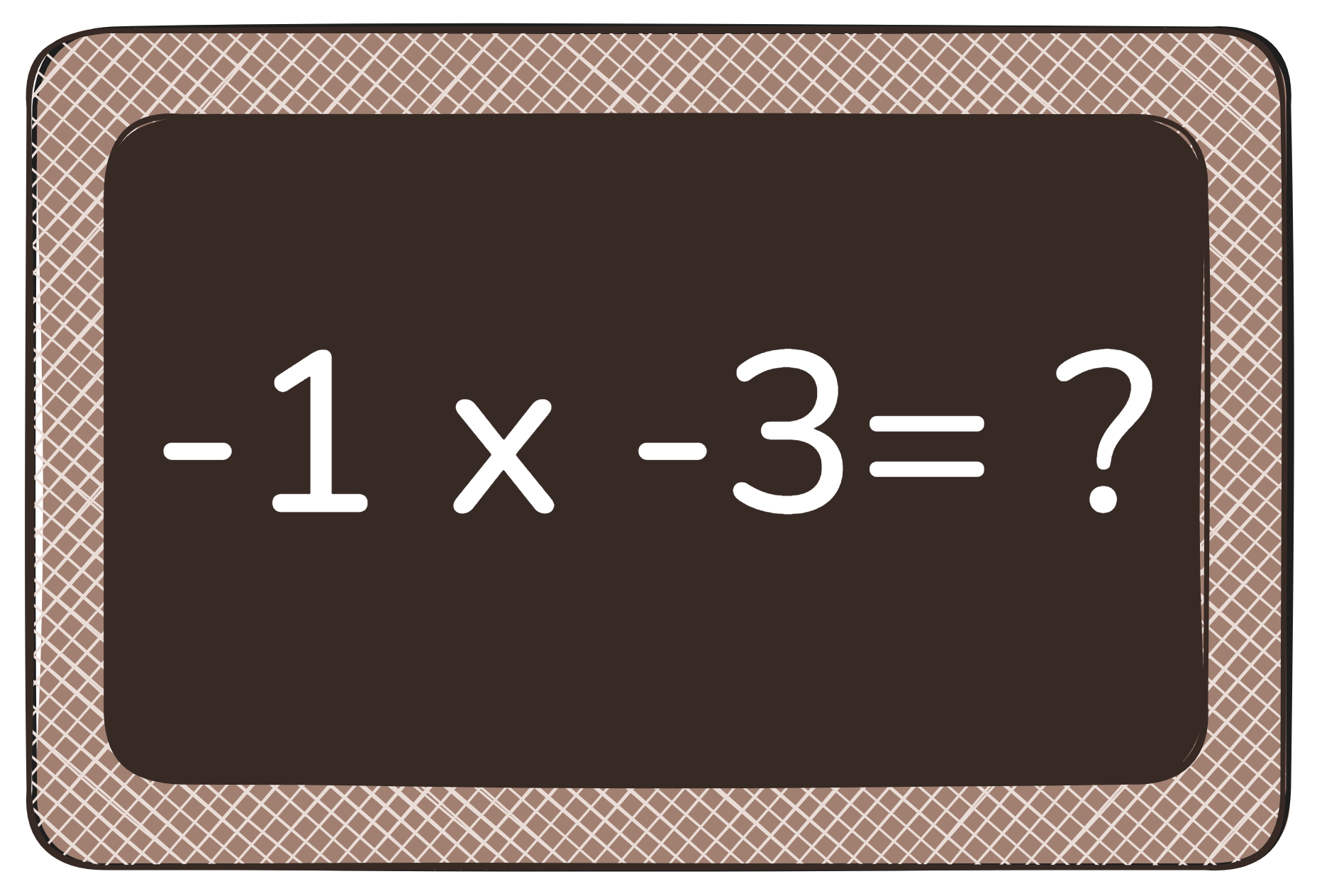Almost everyone remembers the school rule that goes: “minus times minus gives plus.” But have you ever really stopped to wonder where that rule actually comes from? Honestly, I can’t even remember when I learned it—it’s just one of those maths facts we all seem to take for granted.
And yet, if you think about it, it’s not obvious at all! Why should two “minuses” somehow make a “plus?” Is this just something mathematicians decided for convenience, or is there a deeper reason behind it?
Most importantly: can we understand this in a simple, intuitive way—without just memorizing a rule we never quite believed?
Question
If you remove a penalty or a debt from someone, are they better off or worse off?
Why Having a Fine Taken Away Puts a Smile on Your Face
Let’s imagine a creative scenario: take a monkey who gets paid in “banana bucks”—special money she can use to buy her favorite bananas. Every time she gets a banana buck, she has more to spend, and it’s a good day for her!
If she loses a banana buck, however, she’s not so happy—now she can afford fewer treats.
Now, our monkey friend isn’t always on her best behavior. Sometimes she gets into mischief (like throwing banana peels where she shouldn’t, or making a noisy mess in the jungle). When that happens, she gets fined—she has to pay a penalty in bananas.
Here’s where things get interesting: for the monkey, getting a fine is just like losing a banana buck—it’s as if she’s carrying something negative around in her pocket!
So you can think of fines as negative numbers: the more she has, the fewer bananas she’ll end up with.
Now: what happens if someone takes away a fine? If one fine is worth –5 bananas, and someone removes that fine, what does the monkey have now?

The monkey sees something negative disappear—in reality, she’s just gained 5 more bananas! Taking away a debt means you’re actually better off.
In maths terms, if a fine = –5 bananas, and you remove it—that is, you do the negative of a negative (–(–5))—you’re really adding +5 bananas to the monkey’s stash! So –(–5) = +5.
Let’s see with numbers:
- 3 × 5: The monkey gets 3 fines worth 5 bananas each, so +15 bananas.
- 3 × –5: The monkey gets 3 fines worth 5 bananas each, so –15 bananas.
- –3 × –5: The monkey has 3 fines (each –5), but those fines get taken away—so 3 debts are erased, and she ends up with +15 bananas!
This is where maths starts to feel a bit magical: a minus times a minus… really does make a plus! Because getting rid of something negative is almost like receiving a surprise gift.
Challenge
Can you think of other examples where getting rid of something negative actually improves your day?
Now, imagine that the monkey’s banana bucks and fines turn into colored squares: Green squares (banana bucks) are worth +1, red squares (fines) are worth –1. Below, you can try out some simple buttons:
- Add a green square (+1): The monkey gets richer!
- Add a red square (–1): The monkey gets a fine, so her total goes down.
- Remove a green square (+1): The monkey loses a banana buck, so her total decreases.
- Remove a red square (–1): The monkey gets rid of a fine… and her total goes up!
Try it out: watch the total change with each click. What do you notice?
Whenever you remove a penalty (a red square), things get better, not worse! The total goes up—just like the rule “minus times minus gives plus.”
The Number Line and the 180-Degree Flip
As often happens in maths, the same rule can be understood from many different angles. Take multiplying by –1, for example: you can picture it as flipping a number over on the number line, like turning a sheet of paper and seeing the number “mirrored” on the other side.
But let’s ask ourselves: what happens if you flip it twice? You end up exactly where you started!
That’s the reason why minus times minus equals plus: because two flips cancel each other out and leave you with a positive result.
Want to see how this flip works on the number line in real life? This little animation shows that multiplying by a negative number is like making a 180-degree turn on the line. And if you do it twice—a negative of a negative—you’re right back to positive!
Challenge
Drag the arrow anywhere on the line. What happens to it on the number line when you click the ×(–1) button once? And what if you press it twice in a row? What does this show you about how signs work?
What If Minus Times Minus Didn’t Give Plus…?
So far, we’ve seen the “minus times minus gives plus” rule as a sort of magical maths trick. But what if, just for a moment, we changed the rule?
Imagine this scenario: plus times plus gives plus (no surprises), plus times minus gives minus (that’s familiar), minus times plus also gives minus (still makes sense)… but then, minus times minus gives minus again?
Think about what that would mean: the minus sign would become unstoppable—even if you multiplied negatives twice, the result would always stay negative! It would be like a game where “minus” always wins, and “plus” never gets a chance to catch up.
In this world, positive and negative numbers wouldn’t be mirror images of each other anymore. You’d lose the idea of negatives as the “opposite” of positives!
But the need for symmetry isn’t just something mathematicians obsess over—it’s what makes maths rules work everywhere, whether you’re dealing with wallets or debts. It creates a “family” of numbers, where every member has an opposite (like +3 and –3, which together make zero).
That’s why the rule “minus times minus gives plus” is the only real way to keep maths balanced and beautiful!
Not Just a Choice: The Logic Behind “Minus Times Minus Gives Plus”
This rule isn’t just some quirky idea that someone made up: if you want mathematics to hold together—to keep its most important rules like distributivity, symmetry, and opposites—then minus times minus has to give plus.
There’s no trick or shortcut here: it’s the very structure of numbers that demands it!
If we didn’t accept “minus times minus gives plus,” mathematics would end up inconsistent—you couldn’t even trust your times tables or the basic rules of calculation anymore.
Maths, after all, doesn’t make decisions randomly: every rule is built to keep things coherent, elegant, and (most importantly) working.
And the more closely you look, the more you’ll discover that every so-called “weird” rule has a logical reason for being there. Nothing is by chance—there’s always a hidden thread tying it all together, even if it seems mysterious at first glance.
Uncovering More Hidden Secrets in Numbers
How many things do we just take for granted in mathematics—and maybe in our daily lives, too? The rule “minus times minus makes plus” is just one among many; there’s an entire world of “mathematical normality” waiting to be questioned!
Have you ever wondered what would happen if you really could divide by zero, or if “infinity” was just an ordinary number?
In maths, the most important thing isn’t just solving exercises, but looking beyond every rule: often, there’s a conscious choice, a story, a clear reason behind it—and the most valuable question remains “why?”
Question
Are there other arithmetic rules that have always seemed so “obvious” you never even wondered why they work that way?
Activity
Today, pick any rule—even the most basic one (like “why is zero’s sign the way it is?” or “why does multiplication come before addition?”)—and try to turn it upside down. Invent your own alternative mathematics: what challenges would you solve, and what new problems might you create?
BONUS: Multiplication on the Number Line
Have you ever wanted to really see what happens when you multiply by –1, –2, or even by fractions? This interactive tool lets you visually explore how the sign rules work on the number line:
- An arrow starts at zero, and with buttons like “×2”, “×½”, “×–½”, “×–1”, “×–2”, you can watch it change length and direction in real time.
- Multiply by a positive number, and the arrow stretches or shrinks in the same direction.
- Multiply by a negative number, and the arrow does a 180° turn (it flips to the other side of zero)—and may change length, too.
- Try stringing together several multiplications. What patterns or surprises do you notice?
Tip for teachers and parents: Use this applet as a group demonstration in class or at home. Ask students to predict what will happen before you click (“What happens if I multiply by –1? And what if I do it twice? What if I multiply by 2 and then –1?”). This helps everyone connect the abstract maths rules to visuals.
Activities
Maths Experiment: What If the Rule Changed?
Let’s play with an alternative rule: “minus times minus gives minus”!
Try using this new rule and calculate:
a) –3 × –4 =
b) 2 × 6 =
c) –5 × –5 =
d) –7 × +2 =
e) +8 × –3 =
Remember the distributive property? Normally, we know:
3×[2 + (–2)] = 3×2 + 3×(–2)
So:
3×0 = 6+(–6) = 0
Now, calculate –3×[2 + (–2)] in two different ways:
- Directly: –3×0 = ?
- Using distributivity: –3×2 + –3×(–2) = ?
Compare your results: Are they the same, or is something strange going on? If you spot a contradiction, what is it? What’s happening here?
Key Questions
- What happens when you remove a penalty—does what you have increase or decrease?
- If you multiply two negative numbers, is the result positive or negative? Why?
- On the number line, what does “multiplying by –1” mean or look like?
- Imagine you have to explain to a friend why “minus times minus gives plus” without using any numbers. What kind of example would you use?
- If you could make your own maths rules for an alien planet, would you change how the signs work? Why or why not?
Discussion Starters
- When do we use negative numbers in real life?
- Why do you think negative numbers are “on the left” on the number line? What does that position tell us?
- Are all maths rules invented by humans?
- Why do you think nature (and maths) loves balance and symmetry so much? What would happen if there were no “opposites” in maths?
- If you have a debt of 50 euros and someone cancels it, have you gained 50 euros or just returned to zero? Is there a difference? Why?