Con soli 9 fiammiferi, partendo da un semplice triangolo formato da 3 di essi collegati ai vertici da tre palline, riesci a costruire 7 triangoli equilateri?
Indizio
Pensa oltre il piano: i fiammiferi non devono per forza essere disposti tutti su una superficie!
Soluzione
Mancano 6 triangoli da formare usando solo 6 fiammiferi, quindi si può intuire che la soluzione non è una semplice figura piana! Ragionando in 3D, partiamo dal triangolo iniziale di 3 fiammiferi (la base) e proviamo a costruire sopra di esso.
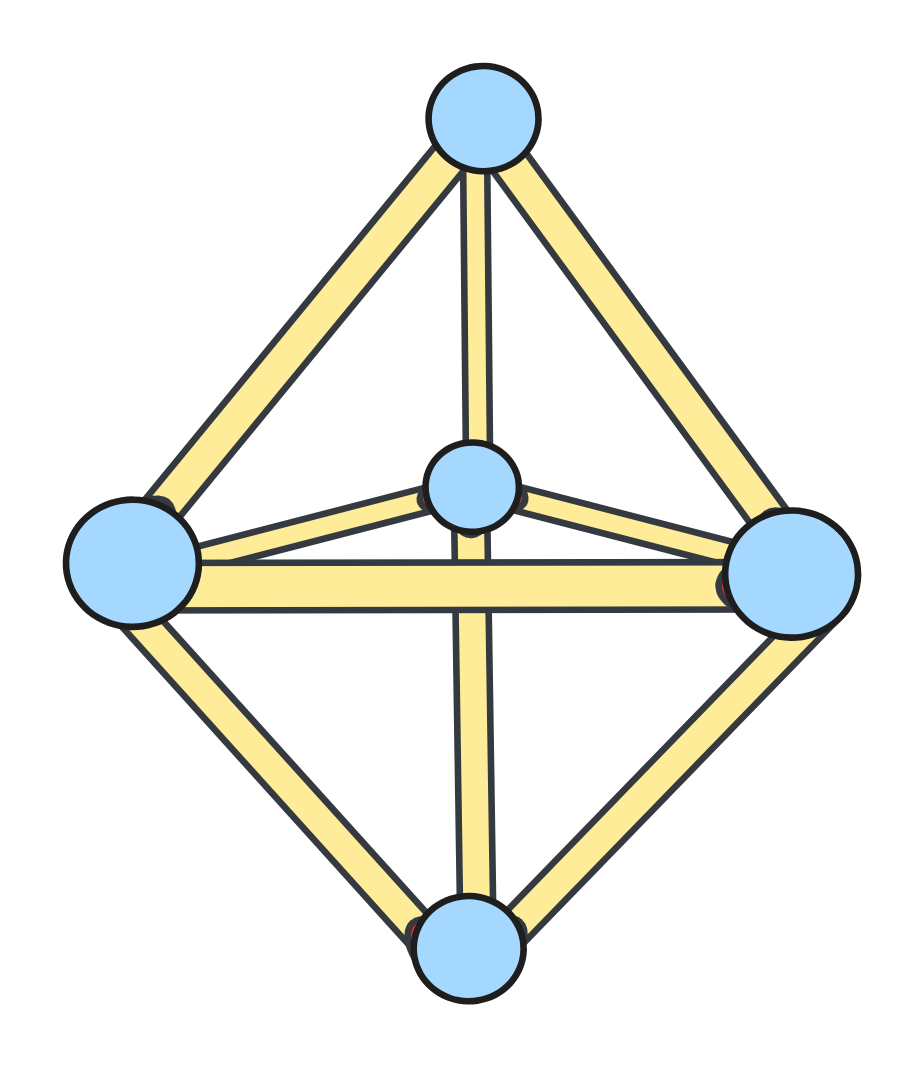
Possiamo aggiungere due fiammiferi a uno dei lati del triangolo di base per creare un nuovo triangolo che condivide quel lato. Se ripetiamo questa operazione per ognuno dei tre lati della base, usiamo 6 fiammiferi in totale e otteniamo 3 nuovi triangoli, ognuno “appoggiato” su un lato diverso del triangolo di partenza. In questo modo formiamo una piramide — un tetraedro — composta da 4 triangoli equilateri (i 3 nuovi più la base).
Per raggiungere i 7 triangoli richiesti, possiamo ripetere la stessa costruzione anche sotto la base: aggiungiamo altri 3 triangoli dall’altra parte, usando gli stessi lati di base. Ora abbiamo una piramide doppia, composta da 7 triangoli equilateri in tutto!